Logical concepts – Rewriting formulas

We can rewrite formulas, with the aim of better understanding the meaning of the logical ‘bones’ (=form) of the statement, and to produce provable formulas, or proofs.

If the rewritten formula has the same meaning as its original formula, both formulas are equivalent (≡). If instead we place a biconditional (↔) between the rewritten and its original formula, and we calculate under this operand, then we get a tautology.

1. Same meaning

Rewriting formulas with operands ˅, ˄, ~
If we use the operands ˅, ˄, ~, which together form a functionally complete set, then we can rewrite these formulas using the following rules (for statements with 2 variables and 1 operand):

Double negative	if A is true, then not not-A is true and its converse: if not not-A is true, then A is true. The rule allows us to introduce or eliminate a negation from a logical proof	~~A ≡ A	|10|
De Morgan’s laws	The negation of a conjunction = the disjunction of the negations	~(A˄B) ≡ (~A˅~B)	|0111|
	The negation of a disjunction = the conjunction of the negations	(~A˄~B) ≡ ~(A˅B)	|0001|
commutativity	changing the order or sequence of the operands within an expression	of disjunctionp˅q ≡ q˅p	|1110|
		of conjunctionp˄q ≡ q˄p	|1000|
	Complete commutative law of equivalence	of biconditional(p↔q) ≡ (q↔p)	|1001|

Rewriting the implication
Expressions that are often used to rewrite the implication.

expression	form	description of the operation	outcome1)	diagram
implication	p→q	first statement implies truth of second	|1011|
contrapositive or transposition	~q→~p	reversal and negation of both statements. (switch the antecedent with the consequent and also negate both)	|1011|
equivalence	~p˅q	p implies q is defined to mean that either p is false or q is true.	|1011|

 2. Different meaning
Expressions opposing/contrary to the implication

expression	form	description of the operation	outcome1)	diagram
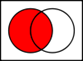
inverse	~p→~q	negation of both statements	|1101|
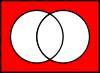
converse	q→p	reversal of both statements	|1101|

Negating the implication

expression	form	description of the operation	outcome1)	diagram
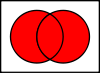
negation	p˄~q	contradicts the implication	|0100|

¹⁾ For spatial efficiency, instead of vertically, I noted the formula’s outcome in the truth table columns horizontally and between ||.

Logical concepts – Tautology and contradiction

Definition: A formula of propositional logic is a tautology if the formula itself is always true regardless of which valuation is used for the propositional variables.

There are infinitely many tautologies.

Example
This formula has only 1 variable, A. To valuate this formula A, we must assign one of the truth values true or false, and assign ~A to the other truth value.

tautology				meaning
A	˅	~	A	Law of excluded middle: for any proposition, either that proposition is true, or its negation is.
T	T	F	T	A or not A
F	T	T	F	not A or A

Verifying with tautologies
Why should we want to have tautologies? A tautology is a semantic way to verify that premises are true as well as their conclusion.

How do we determine whether a formula is a tautology? We 1^st evaluate every variable and then the operand(s) for its possible valuations, till every part of the formula is mapped.  For every variable in a formula, we have 2 values, T and F. If a formula has n variables, then there are 2ⁿ possible valuations of the formula.

For example (A˅B) has 2 variables, then this statement has 2² (=2×2=4) possible valuations. When a statement has 3 variables, then it has 2³ (=2x2x2=8) possible valuations.

Tautological implication
Suppose formula S is a label for formula (A˅(B˅~B)). If R implies S, when every valuation that causes R to be true also causes S to be true, then we have a tautology.

However, suppose formula S is a label for (A˄(B˅~B)). Any valuation that makes A false, will make the formula S false, so that S is not a tautology.

Contradiction
Definition: A contradiction is a statement that is false under all circumstances.

If R is false for all values of its variables, so that there is no truth valuation that causes R to be true, then R is a contradiction.
What happens when we have a contradiction?
For example, in R implies S, the outcome of R→S for R=false, is always true, regardless of the truth or falsity of S. Say R is a label for a formula (p˄~p), which is a contradiction; then R is always false.

contradiction				meaning
p	˄	~	p
T	F	F	T	p and not p
F	F	T	F	not p and p

A contradiction does not eliminate anything, and therefore it implies everything. So a contradiction is useless for purposes of logic or evidence because it is always false, and anything can follow from it.

Deductive logical argument and its form

Deductive arguments are evaluated in terms of their validity and soundness.

Definition: An argument is valid if it is impossible for its premises to be true while its conclusion is false. Or, the conclusion must be necessarily true, if the premises are true. So the premises provide a guarantee for the truth of the conclusion.

The deductive form of Modus ponens
The 1^st form of deductive reasoning is modus (ponendo) ponens, also known as affirming the antecedent. We conclude Q from P by using modus ponens.

P→Q	Is a conditional statement (implication) with antecedent (P) and consequent (Q)
P	Is the hypothesis
∴  Q	The conclusion is deduced from the statement and the hypothesis

Affirming the consequent – a fallacy
If the conclusion (Q) is given instead of the hypothesis (P), there can be no valid conclusion; hence we have the fallacy of affirming the consequent.

Sound argument
Definition: An argument is sound if and only if it is valid and all its premises are true. Otherwise, the argument is unsound.

deductive argument	explanation
All men are mortal.	all objects classified as ‘men’ have the attribute ‘mortal’
Aristotle is a man.	‘Aristotle’ is classified as a ‘man’ – a member of the set ‘men’.
Therefore, Aristotle is mortal	‘Aristotle’ must be ‘mortal’ because he inherits this attribute from his classification as a ‘man’.

Valid, but unsound argument
A deductive argument can still be logically valid, if it has false premises, but then the argument is not sound. Trick arguments are based off of this.

Everyone who eats carrots is a quarterback.	1st, major premise is false, but classifies correctly (everyone)
John eats carrots.	2nd, minor premise: ‘John’ is classified as a member of the set ‘carrot-eaters’
Therefore, John is a quarterback.	‘John’ inherits the attribute ‘is a quarterback’ from his membership; therefore through its form, the conclusion must be true.

Generalizing – a fallacy
Generalizations often make unsound arguments, such as “everyone who eats carrots is a quarterback.” But, since everyone who eats carrots is not a quarterback, such arguments prove the flaw.

In this example, the first statement uses categorical reasoning (the theory of the categorical syllogism. This is the theory of two-premised arguments in which the premises and conclusion share three terms among them, with each proposition containing two of them.), saying that all carrot-eaters are definitely quarterbacks.

When a generalization about all instances of a kind is based on either too few examples which are not known to be typical or based on instances of a different kind, those are called ‘converse accident’, which is the opposite of accident: general.

The fundamental logical concepts – biconditional

Definition: A biconditional is a compound statement formed by combining 2 conditionals under “and.”  Biconditionals are true when both statements have the exact same truth value.

A biconditional actually contains 2 conditional statements. A↔B means (A→B)˄(B→A). Either both are true or neither are true.

How can this we see this?
From 2 conditional statements we can infer a biconditional.
A→B   (if A→B is true)
B→A   (if B→A is true)
∴ A↔B   (then we infer that A↔B is true)

Example
If I’m breathing, then I’m alive
If I’m alive, then I’m breathing
Therefore I’m breathing if and only if I’m alive. Or also: I’m alive if and only if I’m breathing.

And the other way around is also possible: from a biconditional we can infer 2 conditionals.
   A↔B   (iff A↔B is true)
∴ A→B   (then we infer that A→B is true)

   A↔B
∴ B→A   (then we infer that B→A is true)

Example
if it’s true that I’m breathing if and only if I’m alive,
then it’s true that if I’m breathing, I’m alive;
likewise, it’s true that if I’m alive, I’m breathing.

Different interpretations in language:
A biconditional is of the form (A→B)˄(B→A), expressed as A if B and B if A, or A↔B, A if and only if B.
Or we say, A implies B and B implies A.
Sometimes ‘if’ is used as a biconditional, depending on the context.

Examples
I’ll buy you a new wallet if you need one.
If the speaker means with ‘if’, whether or not the wallet is needed, then ‘if’ is meant as a biconditional.

It is cloudy if it is raining.
Since it can be cloudy while it’s not raining, ‘if’ here is not meant as a biconditional. (And also not as a conditional ‘conjunction’, but as a time ‘conjunction’. So correct would be ‘when’.)

biconditional			meaning
A	↔	B	If and only if it rains, the roofs get wet
T	T	T	If and only if it rains, the roofs get wet (if it rains, the roofs get wet; and if the roofs get wet, it rains)
T	F	F	It is not the case that if it rains, then the roofs don’t get wet
F	F	T	It is not the case that if it doesn’t rain, then the roofs get wet
F	T	F	If and only if it doesn’t rain, the roofs don‘t get wet (if it doesn’t rains, the roofs don‘t get wet; and if the roofs don‘t get wet, it doesn’t rain)

The fundamental logical concepts – implication

Definition: The implication is the relationship between the 2 statements of a conditional statement A, called the antecedent and B, called the consequent, when A implies B.

The statement before the arrow is called the antecedent (ante =before) and the statement following the arrow is the consequent (consequī =follow closely). In if A→B, A= the antecedent and B= the consequent.

Other words that indicate a cause-and-effect relationship are:
of cause: as, because, in order that, since, so that.
of condition: even if, if, in case, provided that, unless.
of Time (general): when, while.

In the (material) implication the 2 statements have a different type of relationship with each other than we have seen so far. In a conjunction or disjunction the 2 statements’ order can be reversed while their compound statement’s meaning stays the same. This relation is called commutative. In the implication however, the 2 statements have a cause-and-effect relationship. This means that the order of the 2 statements cannot be reversed without changing the compound statement’s meaning.

If A=T, then B follows from A. But if A=F, intuitively we might think the statement then is irrelevant, or that the resulting truth value is F. However, from A=F, nothing in particular can be inferred from A; B can follow or not.

The logical implication excludes only 1 meaning: cause without effect (A=T, B=F).
Included are: cause and effect (A=T, B=T), effect without cause (A=F, B=T), without both cause and effect (A=F, B=F).

What does it mean if when we say ‘If it rains, the roofs get wet’? Actually it means 4 things. All those 4 statements combined make up the entire meaning of this single statement.

implication			meaning
A	→	B	If it rains, then the roofs get wet
T	T	T	If it rains, then the roofs get wet
T	F	F	It is not the case that if it rains, then the roofs don’t get wet
F	T	T	If it doesn’t rain, then the roofs get wet.[there could be another cause that gets the roofs wet]
F	T	F	If it doesn’t rain, then the roofs don’t get wet.

The fundamental logical concepts

Part 3 – The disjunction

Definition: A logical disjunction is an operation on both statements’ values, that produces the value false if and only if both statements’ values are false. If both statements’ values are true, and if either one of the statements’ values are true, the logical disjunction produces true.

Note that the logical ‘or’ differs from the linguistic ‘or’. The linguistic ‘(either ..) or’ usually means that the statements exclude one another: if one is true then the other is false – or reversed. Depending on the context however, the statements’ values could also be true when both their values are true.

Examples of linguistic disjunctions
– When an advertisement for a lecturing position asks ‘Applicants must have either a PhD or teaching experience’, then also someone who had both a PhD and teaching experience is included.
– When mum tells her son ‘You can either have some candy or some cake,’ she means one or the other, exclusively, and therefore not both.
– ‘Either the chauffeur did it or the butler did it’, can be read both as exclusive and inclusive disjunction.

According to S. Greenbaum in his “Adverbial”, there are 2 kinds of (linguistic) disjuncts: style disjuncts and content disjuncts.
– Style disjuncts are comments made by speakers on the style or manner in which they are speaking [or as an opinion of the speaker.]:
frankly: ‘Frankly, you have no chance of winning’ (= I am telling you this frankly);
personally;
with respect;
if I may say so;
because she told me so: She won’t be there, because she told me so (= I know that because she told me so).
– Content disjuncts comment on the content of what is being said: mostly degrees of certainty and doubt as to what is being said:
‘perhaps’ in ‘Perhaps you can help me’;
undoubtedly;
obviously.

That the logical disjunction always produces the same interpretation, may be viewed as a relief – at any rate less of a headache.

disjunction			meaning
A	˅	B	The sun shines or we have a picnic
T	T	T	The sun shines and we have a picnic
T	T	F	The sun shines, (but) we have no picnic
F	T	T	(Although) the sun doesn’t shine, we have a picnic
F	F	F	It is not the case that the sun doesn’t shine and we have no picnic

So either there is son or a picnic, or both; but excluded as possible interpretation is: no sun and no picnic.

The fundamental logical concepts

Part 2 – The conjunction

Definition: A conjunction is a joint or simultaneous occurrence.

Two things are expressed in 2 statements that are combined with the operand ‘and’. Both these statements are complete sentences, with their own subject and predicate. Although being independent from each other, these 2 main clauses together form 1 joined statement.

Other words that can join (or coordinate) statements are: but, for, nor, or, so, yet

From the 4 logical parts that together make up the conjunction, 3 of them are excluded:
the 1^st sentence with negated 2^nd sentence;
the negated 1^st sentence with 2^nd sentence
the negated 1^st sentence with negated 2^nd sentence.
Included is: the 1^st and 2^nd sentence.

conjunction			meaning
A	˄	B	The sun shines and we have a picnic
T	T	T	The sun shines; we have a picnic
T	F	F	It is not the case that the sun shines and we don’t have a picnic
F	F	T	It is not the case that the sun doesn’t shine and we have a picnic
F	F	F	It is not the case that the sun doesn’t shine and we don’t have a picnic

Logic (10) – The fundamental logical concepts

The base concepts of logic are the conjunction, disjunction, negation and the implication.

Part 1 – The negation

In logic, a simple statement can only have 2 meanings. Either it is the case, which is called ‘true’, or it is not the case, which is called ‘false’. ~p is read as ‘it is not the case that p’.

p And ~p together form a context. If p=T, then ~p=F; and conversely, if ~p=T, then p=F. Since p and ~p exclude each other, they are each other’s complement.

negation		p=the roofs get wet	meaning
~	p
F	T	The roofs get wet	p is T, so ~=F ⇒  p=T
T	F	It is not the case that the roofs get wet	p is F, so ~=T ⇒  p=F

Double negation

In propositional logic, the negation of p‘s negation, is the same as p. Not not p is equivalent to p, expressed in logical symbols: ~~p ≡ p.

A closer look at the implication

It seems necessary to further investigate the 4 possible situations of the example ‘if it rains then the picnic will canceled’. I’ll explain it in propositional logic.

1^st, the implication for this statement has 2×2 values, representing all possible situations; 2 for rain and 2 for  canceled picnic. The 2 variables (A and B, representing rain and cancelled picnic) are placed in 2 columns to compare their possible values. The implication symbol, the arrow, calculates both the variable’s (truth) values. Those values can be expressed in 1 and 0 or True and False.

In logic, if a statement is true, then its negation (~) is false. If a statement is false, then its negation is true.
If A=T then ~A=F.
If A=F then ~A=T.

implication			value	meaning
A	→	B	formulas	If it rains, then the picnic will be canceled
T	T	T	A→B	rain → cancelled picnic
T	F	F	~(A→~B)	It is not the case that if it rains → picnic not cancelled
F	T	T	~(B→~A)	It is not the case that if picnic is cancelled then no rain (picnic cancelled, despite no rain) (=possible)
F	T	F	~B→~A	no cancelled picnic → no rain

Notice that A→B logically means exactly the same as ~B→~A the difference is that A→B is stated affirmative and ~B→~A is stated negative. ~B→~A is called the contrapositive of A→B, which is a direct statement.

Although A=T and B=F in ~(A→~B), since the whole statement is negated, its outcome is denied.

Although B=T and A=F in ~(B→~A), since the whole statement is also negated, there is a possibility. The not-raining is detached as sole cause for the cancelled picnic. Since this valid possibility of the implication is not an intuitive formula, it is easily overlooked. Hence, the thought that if the antecedent is denied, that thus follows the consequent has to be denied as well.

Subvert the argument – a fallacy

‘If it rains, the picnic will be cancelled.’

This argument is often interpreted as: If it does not rain, the picnic will go on.

What assumption is made?
The reasoning behind it is, that if the first part of the argument is negated (or denied), then the consequence will be denied as well. So, if it does not rain, it automatically means the picnic will go on.

Why is this deduction wrong?
Let’s start with what this argument exactly means.
‘If’ is the condition,
‘it rains’ is the antecedent (the cause);
‘the picnic will be cancelled’ is the consequent (the effect).

Expressing the assumption in capital letters:
If A then not B  (if the condition is it rains, then there’s no picnic)
Not A                (the situation is it does not rain)
Thus: not B       (then there is not no picnic = double negation = positive; so there is picnic)

The implication has 4 possible outcomes, because the antecedent as well as the consequent can be affirmed or negated. The condition (if) calculates the possible result from these affirmations and negations.

If A then not B  (if the condition is it rains, then there’s no picnic)
1. A                   (rain)
Thus: not B       (no picnic) This conclusion is valid; the implication says: if it rains, then no picnic.

2. A                    (rain)
Thus: B              (a picnic) This conclusion is impossible; the implication says: if it rains, then no picnic.

3. not A              (no rain)
Thus: B              (a picnic) This conclusion is valid. It is possible that there is a picnic if it doesn’t rain.

4. not A              (no rain)
Thus: not B        (not no picnic) This conclusion is valid too; both parts of the argument are negated. It is also possible that there is another reason than no rain why there is a picnic.

What is wrong about denying the antecedent is: it assigns only 1 cause (rain) to the effect (no picnic) and thus other possibilities (for no picnic) are dismissed.

The fallacy of subverting the argument – or denying the antecedent, as it’s also called – is that it undermines or disrupts logic (deliberately or accidentally). It thereby shrinks reality’s possibilities.

I know, we all want to reduce the information, but if that’s done by not taking something into account that we should, then that might have unanticipated or unwanted consequences. To reduce the information effectively we apply logic, so we can truly anticipate.